SIRC Solar System

This is a summary of my Science in the River City workshop aimed
at fifth-grade solar system standards.

I started by projecting this opinion piece responding to the release
of a new survey showing that 26% of Americans answered the question
"Does the Earth go around the Sun, or does the Sun go around the
Earth?" incorrectly.  The opinion piece was a bit snarky and
unforgiving; educators know that everyday experience (eg, seeing the
Sun rise and set) is extremely powerful.  People who think the Sun
goes around the Earth are at least processing what they see and
building some kind of model to account for it. The vast majority of
people who "know" that the Earth goes around the Sun are probably just
memorizing something their teachers told them, and probably could not
cite evidence or build an argument to support this statement.  But the
latter is a much more valuable skill in today's society, and the Next
Generation Science Standards (NGSS) call for our kids to practice this skill.
So, I asked the teachers to role-play in pairs, one building an
argument that the Sun goes around the Earth and the other vice
versa. Try it...it's hard!

The #1 argument for Sun-around-Earth is, of course, rising and
setting, but there aren't a lot of obvious strong arguments for the
other way.  Kids will try to invoke authority, such as "NASA launches
rockets that can see what's going on" but I steer them away from that;
people concluded Earth-around-Sun long before rockets were built, so
they should be able to use simpler observations.  One pair of teachers
played out the two models using their bodies so they could see the
consequences of each, and that's exactly what I recommend whenever
possible.  They showed that the Sun's daily motion could be explained
by the Sun-around-Earth model or by a spinning-Earth model (which is
not the same as Earth-around-Sun).  Lesson: don't stop creating models
once you find one that fits, as other models might fit the data too!

If we had no other data, we might not be able to choose between these
models.  In such cases we should try to bring other observations to
bear, and/or deduce further consequences of each model. An example of
the latter: if the Earth is spinning, why don't we feel it?  We feel
dizzy when we spin on a merry-go-round....but if the merry-go-round
took 24 hours to complete one turn the effects might be too small to
feel.  So that was worth thinking about, but inconclusive. Can we
bring other data to bear? Well, just about everything in the night sky
rises and sets and rises again in about 24 hours, so the
Sun-around-Earth model has to become the
entire-universe-turns-around-Earth model.  But it's a lot easier to
believe that one thing (Earth) spins than that everything in the
universe contrives to revolve around Earth in 24 hours. Preferring the
simpler model is called Occam's razor, and we do that all the
time in real life. (Think of situations where someone is caught
red-handed doing something they shouldn't, and they say "This isn't
what it looks like" and tell a complicated story...do you believe the
simple story or the complicated story?)

The real physical proof that the Earth spins is quite subtle. One is the
Coriolis effect: we can measure the effects of being on a slowly spinning
"merry-go-round".  I showed the teachers a great kinesthetic activity
for this (described in a previous post).  Another is the Foucault
pendulum, which is not easy to demonstrate in a school but which kids
may have seen in science museums.  A third is even more modern:
astronomers can directly measure velocities of celestial objects using
the Doppler shift (the same principle is used by radar speed guns),
and we constantly have to correct for the velocity of the observatory.
Because of Earth's rotation, stars that are rising appear to be moving toward
us and stars that are setting appear to be moving away from us.

So the Earth spinning accounts for the daily (apparent) motions of Sun
and stars...so why do we think Earth goes around the Sun? (Do you see
how much reasoning we had to do to even get to this question?) Anyone
who looks at the stars periodically must have noticed that you can't
see the same stars all year round.  And because the presence of the
Sun in the sky defines when we can't see stars, that means that the
Sun moves relative to the stars.  Another way to say this is that,
unlike the Sun, the stars don't take exactly 24 hours to (appear to)
go around; they take 23 hours and 56 minutes.  So the Sun may be
opposite a certain star (ie the star is high up at midnight) at a
certain time of year, but over months will creep around the sky to
prevent us from seeing that star, and after 365 days the Sun will be
back to its original position relative to the stars.  Earth's rotation
period is either 24:00 or 23:56; it can't be both!  (It could be
neither, but considering that possibility may cause cognitive
overload.)

If we again use majority rule or Occam's razor, it's simpler to think
that the stars are fixed and that the Sun moves relative to the Earth
(note how little this conclusion has to do with the basic observation
that the Sun rises and sets each day, which is caused by Earth
spinning).  But there are at least two models which involve the Sun
moving relative to Earth, and again I had teachers play the roles of
Sun and Earth to demonstrate a model where Sun is stationary and Earth
moves, and vice versa.  Both of these models account for the
observations equally well (so far), and the moving-Earth model has the
disadvantage that we don't feel the Earth move.  This is one reason
many ancient Greek thinkers did not endorse the moving-Earth
hypothesis. But Galileo figured out that if you are in a laboratory
moving at constant velocity, you can't feel it move---think of a smooth plane
ride at 500 mph.  Earth doesn't move at constant velocity, but it changes its
velocity so slowly that the effects are really small.

The other thing the ancient Greeks figured out is that the
moving-Earth hypothesis means that we should see parallax. Think about
sitting in a moving car.  The roadside trees appear to rush by, but
the distant mountains appear to move very slowly.  If the Earth moves,
we ought to be able to see an effect like this by comparing nearby and
distant stars.  I taped some stars around the room and some teachers
played this out.  If Earth is still, we will not see parallax.  The
Greeks looked for parallax but did not see it, so they favored the
stationary-Earth hypothesis; they weren't stupid!  It just turned out
that even the nearest stars are so far away that the parallax effect is
tiny and could not be measured until modern times.

Using parallax we can determine that the nearest star is about 300,000
times more distant than the Earth-Sun distance (that comparison is natural
because it is Earth's motion over that distance that gives rise to the parallax
effect).  It's as if your car moved one mile but you were asked to discern the
difference in your view of mountains 300,000 miles away (eg, on the
Moon).  This can be illustrated dramatically by drawing a one-inch
Earth-Sun model on the board, and then drawing a long line
representing the distance to the next star and asking the kids to stop
me when they thought I had arrived.  Kids (even most adults) have no
idea how much 300,000 times is; they ask me to stop after 5 feet or
so, but I keep going.  When I run out of board, I get a roll of toilet
paper and start unrolling it, as a way to illustrate a very long line.
I keep going even when they tell me to stop. Then, when I run out of
toilet paper, I go to the back room and get a cart full of hundreds of
rolls of toilet paper!  It is really dramatic and fun. It's also fun
to write out the number of miles to the next nearest star on the
board: about 24,000,000,000,000 miles. (Kids and even most adults have
little idea what a "trillion" really means.)

Finally, because a light looks dimmer the greater its distance from
us, we can calculate how much light a typical star emits (as opposed
to the very small amount of its light that we receive).  Correcting
for this distance factor, it turns out that stars emit about as much
light as our Sun!  Some emit more, some less, but the bottom line is
that each star is a sun unto itself, or if you prefer, the Sun is just
another star.  In the 1600's, long before parallax was ever measured,
the astronomer Christiaan Huygens turned this argument on its head:
assuming the star Sirius is as luminous as our Sun, how far away would
it have to be to appear so dim?  His conclusion was 30,000 times as
far as the Sun; this is lower than the true value, but only because Sirius is
actually substantially more luminous than the Sun.  And his number was
certainly big enough to convey some of the vastness of the universe.

The Moon does go around the Earth, so we used that to address the
gravity standard.  I did the donutapult demo, which illustrates that
for anything to move in a circle there must be a force directed toward
its center; therefore the Moon is pulled on by a force directed toward
Earth's center.  We can relate that to gravity (ie, the force we feel
every day here on Earth's surface) by looking at a globe and noting
that, anywhere on Earth, "down" means toward the center of the Earth.
Therefore (Occam's razor again) we don't need to hypothesize about a
mysterious force keeping the Moon in its orbit; it could well be the
same force that makes apples fall. (Proving that it's the same force
goes beyond the fifth grade standards.)

Finally, we discussed scale models, as scale is a crosscutting concept
in the NGSS. There is no better way to make people appreciate how
empty space is than to build a scale model of the solar system! Rather
than write up our discussion, I refer you to my previous blog posts on
the scale model project I led at Peregrine School: intro, poster assignment,
and completion.

A few links you may find useful:

• my previous SIRC workshop on the solar system (8th grade)
• Powers of Ten video to help students appreciate scale
• interactive tool to do the same (Warning: this tool only shows relative sizes, not the huge distances between celestial objects)
• feel free to browse the labels at right

Climate 101B: Uncertainty and Model-independence

Following up on my previous post, a few more points are worth making
regarding the scientific process.

First, regarding uncertainty.  Earth's atmosphere and oceans do form a
more complicated system than the simple model I described.  For
example, here's one way in which it is possible that temperatures
would not rise much in response to carbon dioxide impeding the outward
flow of heat.  When temperatures go up initially, that means more
water vapor in the atmosphere.  If that water vapor condenses into
clouds, the extra clouds could reflect enough sunlight back into space
to reduce the heating and make temperatures fall back to normal.  This
mechanism would act like a thermostat keeping Earth's surface within a
narrow temperature range, and we wouldn't need to worry about keeping
our carbon emissions in check.  So, if you heard Arrhenius's warming
prediction in 1896, you could easily say, "but there's a lot of
uncertainty in that prediction because we don't understand cloud
formation.  Maybe there won't be that much warming.  It's uncertain."

The point I want to make is that uncertainty cuts both ways. Water
vapor is itself a greenhouse gas, so if the extra vapor does not
condense into clouds, the greenhouse warming will be accelerated.
Yes, the prediction is uncertain....but that means that more extreme
outcomes, as well as less extreme outcomes, are possible.

If a little bit of warming produces clouds which shut down further
warming, we would call that a negative feedback loop; negative because
any change contains the seeds of its own reversal.  If instead a bit
of warming creates water vapor which accelerates the warming, we would
call that a positive feedback loop; positive because a little movement
encourages further movement in the same direction.  One reason climate
is complicated is that it is full of feedback loops, another example
being that reduced ice coverage causes more sunlight to be absorbed,
which reduces ice coverage further, etc.  So what's the verdict on the
cloud formation?  We still don't know; it may depend on how much
small-particle pollution we produce, because these small particles
provide the seeds for cloud condensation.  But meanwhile, temperatures
keep rising.  So while we puzzle over the details, let's not forget
the big picture: we keep making Earth's carbon-dioxide blanket thicker
and thicker.

Second point: I've repeatedly stressed the important of models in terms of
understanding a system. Models are great for exploring a variety of
scenarios, but is there anything we can say about climate that does
not depend on what model we adopt?  Such model-independent statements
can be valuable anchors when we're not sure which model to adopt.  I'd
like to focus particularly on a (more or less) model-independent
statement regarding sea levels.  We can get rid of models and just
accumulate data regarding sea levels and carbon dioxide levels in the
past, and then we can simply ask, what is the typical sea level when
the carbon dioxide level is 400 parts per million, as we have now
caused it to be? (It's up from about 275 before the Industrial
Revolution.)

The answer is shocking: 24 meters, or 80 feet!  Go ahead and play with
this interactive flood map to see what such a rise will do to your
state or country.

Now I have to give a few caveats. First, changes in carbon dioxide
concentration and sea levels occurred very slowly in the past.
Although we are pumping carbon dioxide in very quickly, it's quite
likely that it will be hundreds or even a few thousand years before
the effects of the carbon input are fully realized and sea levels rise
this much.  Essentially no one is predicting these sea levels within
our children's lifetimes.  But still....this will be a lot for our
great-great-grandchildren to deal with.  And yes, there's uncertainty on this
prediction. Sea levels may rise less than this.  But they may also rise more
than this.

Second caveat: this prediction is not entirely model-independent. To
be an extreme devil's advocate, if CO2 levels in the past were somehow
a natural effect of higher sea levels rather than a cause, then we could not
use past data to predict what would happen when we artificially increase
CO2 levels today.  To be clear, I invoke that scenario not because I
believe it, but simply to highlight how an apparently
model-independent statement is often not entirely
model-independent. If all kinds of crazy models are allowed into the
discussion, then very few truly model-independent statements can be
made.  But within the scope of "reasonable" models, we can say that
sea levels will rise by around 24 meters; we just don't know long
that will take.  Predicting how long it will take requires a model!

If you are interested in further reading, start with this Skeptical
Science post, which summarizes this publication in an approachable
way.  Skeptical Science, by the way, is a good resource for rebutting
common climate myths.

Climate 101

Nice article today in the New York Times: Study Links Temperature to a 
Peruvian Glacier’s Growth and Retreat. It's a good example of how news
about climate change could easily be misread as indicating more doubt
than there really is.  The headline makes it sound as if the link between
glaciers and temperature is so tenuous that this is the first evidence of it,
and that it has been established for only one glacier.  The truth is very
different, even though the headline and article are not wrong once you
understand the context. This post is aimed at helping teachers
and students with the basics, and then use that to parse the news.

Over a century ago, it was known that carbon dioxide impedes the flow
of heat (in the form of infrared light) from the Earth out into space,
while not impeding the flow of heat (mostly in the form of visible
light) from the Sun to the Earth.  If not for this natural greenhouse
effect, Earth would be much colder.  Teachers can demonstrate quite
directly that carbon dioxide impedes the flow of infrared light, but
many teachers may not have the right equipment.  Here's a video
comparing the temperature rise of two bottles, one with elevated
levels of carbon dioxide and the other with standard air.  And here's
a nice video using an infrared camera to show quite directly that
infrared light is largely blocked by carbon dioxide.

Around the same time (1896) Svante Arrhenius recognized that humans
were pumping ever more carbon dioxide into the atmosphere, and that
this would lead to warming.  But "warming" sounded reasonably
beneficial, especially given Arrhenius's prediction that it would take
place slowly over thousands of years.  Arrhenius did not account for
the large increase in population over the ensuing century, nor for the
large increase in per-capita use of fossil fuels (cars, airplanes,
etc). Worldwide, we now emit about 17 times the carbon dioxide emitted
in 1896, so change is coming much faster.  And now we know that an
increase in temperature is not as beneficial as it may sound because
it can radically change weather patterns, which imposes large costs on
humans as well as on many species which cannot move and adapt rapidly
enough.  Apart from that, Arrhenius deserves kudos for his prescience.

Yet if we heard this prediction in 1896 we would be justified in
expressing some skepticism. Earth's atmosphere and oceans (where most
of the excess heat is deposited) form a complicated system, and the
response of a complicated system to a simple input (more heat) may
well not be a simple result (higher temperature).  But healthy
skepticism goes only so far; unless you have a better model, you have
to admit that the best model predicts warming.  Just saying "it's a
complicated system" does not give you the right to reject all models.
In this case, you would have to figure out where the extra heat would
go without causing increased temperatures, and you would have to have
some evidence to motivate belief in that model.

Fast forward to 2014.  Warming is here, and we've learned a lot about
climate models in the meantime. We did find complications (El Nino,
for one), but the simple model was reasonable in its overall
prediction.  More heat does mean a higher temperature.

One way "climate skeptics" (I put the term in quotes because
oil-company funding leads to a kind of "skepticism" different from the
detached sort of skepticism we encourage in science) sow doubt about
this result is to suggest that the warming may be due to natural
cycles.  There certainly are natural climate cycles, but rather than
treat them in detail here I want to make a bigger point about how
science works: When a model makes a prediction and the prediction
comes true, we should gain confidence in the model, and we should lose
confidence in models which made contrary predictions. Yes, it's
conceivable that the greenhouse model's prediction came true through
a fluke of natural cycles rather than accurately modeling how nature works
...but how much confidence would you put on that possibility? 

A prediction is a powerful thing, so let's note the distinction between
a prediction and a retrodiction (or postdiction), which is when you make a
hypothesis after looking at the data.  Using data (rather than laws of
physics or other guiding principles) to generate hypotheses is a fine
thing to do, but because "patterns" can randomly appear in data you
cannot confirm the hypothesis with the same data which generated it;
you must seek out new data. (Admittedly, even scientists sometimes
forget to apply this principle.)  Climate skeptics can suggest
alternative causes for the warming after looking at the data, but we
should have much more confidence in the model which actually predicted
the data.

Now, the news: a reconstruction of the timeline of growth and
shrinkage of a Peruvian glacier shows that shrinkage is most highly
correlated with temperature and not with other factors such as
precipitation.  You have to get halfway through the article to get the
background:

land ice is melting virtually everywhere on the planet...the pace seems to have accelerated substantially in recent decades as human emissions have begun to overwhelm the natural cycles. In the middle and high latitudes, from Switzerland to Alaska, a half-century of careful glaciology has established that temperature is the main factor controlling the growth and recession of glaciers. But the picture has been murkier in the tropics. There, too, glaciers are retreating, but scientists have had more trouble sorting out exactly why. 

So, you may have started reading the article thinking that scientists
understood very little about glaciers if they were just now finding a
"link" between glacier shrinkage and temperature, but you now see
that a lot of important knowledge has already been established.
Newspaper articles are designed to tell you what's new first, so it's not
the writer's fault that this background was buried deep in the article.
Nevertheless, in practice many readers will just read the headline and
skim the first part of the article, thus missing this crucial background.
Teachers and students should be aware of this when reading science news.

But wait, there's more! The article goes on to explain how the details
of tropical glaciers are different from most glaciers (intense
sunlight can vaporize the ice directly, and the sunlight lasts
year-round) but that one group of scientists has studied the matter
and still concluded that temperature is the driving factor in
shrinking tropical glaciers. "But a second group believes that in some
circumstances, at least, a tropical glacier’s long-term fate may
reflect other factors. In particular, these scientists believe big
changes in precipitation can sometimes have more of a role than
temperature."  In other words, this is a legitimate scientific dispute, but
it is about the details of a very specific type of glacier and has little or
nothing to do with overall concerns about glaciers (or sea ice)
melting worldwide, much less about the reality of climate change.  Yet
someone who wants to sow doubt about climate change can point to this
and say "scientists don't really understand why glaciers melt" and people
who don't read the article carefully may well be snookered by that.
Please make sure you (and, if you are a teacher, your students) don't
get snookered.

My next post discusses two more aspects of the nature of science---uncertainty
and model-independent statements---in the context of climate.

One Percenters

We've been bombarded all winter with stories of cold and snowy weather in the eastern US, but the news was just released that January 2014 was the fourth-warmest January on record.  How can this be? The eastern US covers less than 1% of the Earth's area, so (as this essay nicely puts it) "if the whole country somehow froze solid one January, that would not move the needle on global temperatures much at all."  That essay is worth reading because it goes on to explain how subjectively people do perceive global warming: something as unrelated to global warming as being in a cold room does have an influence on the opinions voiced in a survey.   Educators should be aware of this, and actively work on making students think objectively and use data.

Mostly Harmless

In the Hitchhiker's Guide to the Galaxy, "mostly harmless" is the
Encyclopedia Galactica's assessment of Earth (which is not important
enough to merit a longer entry).  This made me think that looking at
the solar system through alien's eyes might help students learn about
it.  I conducted Science in the River City workshop for earth science
teachers based on this idea, and this is a list of resources for such
teachers.

First, I highlighted a graphing activity I had done with elementary
kids; that experienced is described in great detail here. (Feel free
to download and copy the graph.)  I extended the activity to graphing the
surface temperatures of the planets as a function of distance from the
Sun, which led to the greenhouse effect discussion below, but now it
occurs to me that a great way to extend this activity would be to jigsaw
it: assign one group of students to graph size vs distance from the Sun,
another to graph temperature vs distance from the Sun, another to graph
density vs distance from the Sun, etc, and then the groups come together
to think about what it all implies for the formation of the solar system.

Second, when discussing the formation of the solar system and

describing how small grains of dust started to stick together, I

wanted to show a video clip but had some technical difficulties.  Here

is the link; start at 3 minutes into the video and go for 2.5 minutes.

(If you have time, the whole episode is worth watching.  It's from the

How the Earth Was Made series, which has some really nice

visualizations and is constructed around evidence, which is a key

feature missing from many science documentaries.  It tells science

like the detective story it is.  That's generally a good thing, but in

this case the implication that this particular astronaut doing this

particular demonstration singlehandedly saved the theory is a bit of

an exaggeration.)

Pocket solar system: https://nightsky.jpl.nasa.gov/download-view.cfm?Doc_ID=392

Peppercorn Earth: http://www.noao.edu/education/peppercorn/pcmain.html

Extrasolar planets: http://exoplanets.org/ has the most up-to-date

info. Even better, they have built-in graphing tools so you and

your students can easily explore the data.

Earth's surface temperature: I got my plot from the most authoritative

source for modern temperatures, NASA's Goddard Institute for Space Studies.

This link only scratches the surface of climate change data because it deals

with modern temperature measurements (as opposed to long-ago temperatures

inferred from ice cores etc) but as the greenhouse effect was not the focus of

the workshop I won't try to compile a list of links here.  (For those

not attending the workshop: we graphed planets' surface temperatures

vs distance from the Sun, and we saw the general pattern that farther

from Sun equals colder, but we also saw that Venus is a real outlier

from this pattern.  That's because Venus has had a runaway greenhouse

effect.  Earth also has a natural greenhouse effect which keeps us

from being frozen, but which is now being augmented by a manmade

greenhouse effect.  I did tell the teachers that Earth has a "carbon

cycle" which will absorb the extra carbon dioxide through the oceans

into rocks, but I forgot to mention that it will take hundreds of

thousands of years; I didn't mean to imply that humans can carry on

regardless. Venus' greenhouse effect is "runaway" because its

carbon cycle shut down when its oceans boiled.)

Finally, a few links I didn't get time to show but which will help you

appreciate the size of the universe (and the sizes of things in it):

the classic Powers of Ten video and an interactive tool.

One Plus z

This marks the launch of a new series of posts, aimed at astronomy and physics majors. In the course of my teaching I've noticed a few topics---such as propagation of errors and reduced mass---which seem to fall through the cracks between classes.  Students hear a bit about reduced mass in more than one class, but never seem to get a satisfying explanation in any one class.  Their lab instructor taught them how to propagate errors but never made them think about why.  And so on.  This first post is much more specific---how to think about redshifts and velocity dispersions in cosmology---but fits the bill because it seems to fall through the cracks between textbooks.  Practitioners know that "you need to divide by 1+z" but documentation of this is hard to come by.  So here we go.

In cosmology, we often want to measure the rest-frame velocity dispersion of a galaxy cluster, but what we actually measure is the redshift dispersion. How are they related? Redshift z is defined in terms of emitted and observed wavelengths as

This means that 1+z is a stretching factor; it is the ratio of observed to emitted wavelengths.  So you will see the combination 1+z over and over, rather than z by itself.  Get used to thinking in terms of 1+z!

The Doppler shift formula tells us the wavelength stretching factor in terms of velocity:

You will often see this called the relativistic Doppler formula, as opposed to the simpler low-velocity approximation used in many situations. But I suggest thinking of this as the Doppler formula because  high velocities are common in astrophysics, and this correct version is simple enough to memorize. Habitually using the low-velocity approximation can get you in trouble.

The Doppler formula can be inverted to obtain

Now imagine two galaxies, one at rest¹ in the cluster frame (with velocity v₁ in our frame) and a second moving with some velocity v₂₁ relative to the cluster which implies some velocity v₂ in our frame.  According to the Einstein velocity addition law,

Substituting the inverted Doppler formula into this, we obtain a complicated-looking expression for v₂₁/c:

which we can simplify in a few steps:

Because of my poor equation formatting, I have to remind you here that this is an expression for v₂₁/c, where v₂₁ represents a velocity in the cluster frame rather than in our frame. This gets us close to our goal because we want to know the velocity dispersion in the cluster frame. But this is as far as we can go without an approximation. A useful approximation in this context is that so define and eliminate z₂ using :

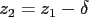Taylor expanding this about we obtain

This is true for any small redshift difference, so it must be true if delta represents the redshift dispersion of the cluster (thus making v₂₁ represent the velocity dispersion of the cluster). Therefore

However, there is a much more elegant way to derive the same result. Imagine a hypothetical observer on the first galaxy. Because of the definition of 1+z as the ratio of wavelengths, it must be true that 1+z₂ = (1+z₁)(1+z₂₁) where z₂₁ is the redshift of galaxy 2 as seen by galaxy 1 (z₁ and z₂ are, as before, redshifts seen by us). Therefore

Again we use an approximation: so that we can use the low-velocity approximation for the Doppler shift, . Therefore

which is the same result as before.  We don't actually need special-relativistic reasoning if we simply use the definition of redshift to isolate the one nonrelativistic velocity in the problem.

We can better expose the equivalence of these two approaches by taking the idea of daisy-chaining wavelength ratios and applying it directly to the Doppler law:

This just says that galaxy 2's wavelength ratio ("ratio'' here is relative to a laboratory standard) observed by us is its wavelength ratio observed by galaxy 1, times galaxy 1's wavelength ratio observed by us.   In a few lines of algebra, you can show that the above expression leads directly to the Einstein velocity addition law.  The addition law can be derived in more than one way, but to me this is the most intuitive way.  Thus, daisy-chaining Doppler factors and using the velocity addition law are not contrasting approaches; they are actually the same thing.

Exercise for the reader: show that the expression above does indeed lead to the Einstein velocity addition law.

Footnotes:
¹ I specify "at rest" here only so that later it will be easy to think of this galaxy’s redshift as the mean cluster redshift.