This marks the launch of a new series of posts, aimed at astronomy and physics majors. In the course of my teaching I've noticed a few topics---such as propagation of errors and reduced mass---which seem to fall through the cracks between classes. Students hear a bit about reduced mass in more than one class, but never seem to get a satisfying explanation in any one class. Their lab instructor taught them how to propagate errors but never made them think about why. And so on. This first post is much more specific---how to think about redshifts and velocity dispersions in cosmology---but fits the bill because it seems to fall through the cracks between textbooks. Practitioners know that "you need to divide by 1+z" but documentation of this is hard to come by. So here we go.
In cosmology, we often want to measure the rest-frame velocity dispersion of a
galaxy cluster, but what we actually measure is the redshift
dispersion. How are they related? Redshift
z is defined in terms of emitted and observed wavelengths as
This means that 1+z is a stretching factor; it is the ratio of observed to emitted wavelengths. So you will see the combination 1+z over and over, rather than z by itself. Get used to thinking in terms of 1+z!
The Doppler shift formula tells us the wavelength stretching factor in terms of velocity:
You will often see this called the relativistic Doppler formula, as opposed to the simpler low-velocity approximation used in many situations. But I suggest thinking of this as
the Doppler formula because high velocities are common in astrophysics, and this correct version is simple enough to memorize. Habitually using the low-velocity approximation can get you in trouble.
The Doppler formula can be inverted to obtain
Now imagine two galaxies, one at rest
1 in the cluster frame (with velocity v
1 in our frame) and a second moving with some velocity v
21 relative to the cluster which implies some velocity v
2 in our frame. According to the Einstein velocity addition law,
Substituting the inverted Doppler formula into this, we obtain a complicated-looking expression for v
21/c:
which we can simplify in a few steps:
Because of my poor equation formatting, I have to remind you here that this is an expression for v
21/c, where v
21 represents a velocity in the cluster frame rather than in our frame. This gets us close to our goal because we want to know the velocity dispersion in the cluster frame.
But this is as far as we can go without an approximation. A useful approximation in this context
is that

so define

and eliminate z
2 using
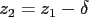
:
Taylor expanding this about

we obtain
This is true for any small redshift difference, so it must be true if delta represents the redshift dispersion of the cluster (thus making v
21 represent the velocity dispersion of the cluster). Therefore
However, there is a much more elegant way to derive the same result. Imagine a hypothetical observer on the first galaxy. Because of the definition of 1+z as the ratio of wavelengths, it must be true that 1+z
2 = (1+z
1)(1+z
21) where z
21 is the redshift of galaxy 2 as seen by galaxy 1 (z
1 and z
2 are, as before, redshifts seen by us). Therefore
Again we use an approximation:

so that we can use the low-velocity approximation for the Doppler shift,

.
Therefore
which is the same result as before. We don't actually need special-relativistic reasoning if we simply use the definition of redshift to isolate the one nonrelativistic velocity in the problem.
We can better expose the equivalence of these two approaches by taking the idea of daisy-chaining wavelength ratios and applying it directly to the Doppler law:
This just says that galaxy 2's wavelength ratio ("ratio'' here is relative to a laboratory standard) observed by us is its wavelength ratio observed by galaxy 1, times galaxy 1's wavelength ratio observed by us. In a few lines of algebra, you can show that the above expression leads directly to the Einstein velocity addition law. The addition law can be derived in more than one way, but to me this is the most intuitive way. Thus, daisy-chaining Doppler factors and using the velocity addition law are not contrasting approaches; they are actually the
same thing.
Exercise for the reader: show that the expression above does indeed lead to the Einstein velocity addition law.
Footnotes:
1 I specify "at rest" here only so that later it will be easy to think of this galaxy’s redshift as the mean cluster redshift.







 so define
so define  and eliminate z2 using
and eliminate z2 using 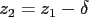 :
:

 we obtain
we obtain


 so that we can use the low-velocity approximation for the Doppler shift,
so that we can use the low-velocity approximation for the Doppler shift,  .
Therefore
.
Therefore
