Mostly Harmless

In the Hitchhiker's Guide to the Galaxy, "mostly harmless" is the
Encyclopedia Galactica's assessment of Earth (which is not important
enough to merit a longer entry).  This made me think that looking at
the solar system through alien's eyes might help students learn about
it.  I conducted Science in the River City workshop for earth science
teachers based on this idea, and this is a list of resources for such
teachers.

First, I highlighted a graphing activity I had done with elementary
kids; that experienced is described in great detail here. (Feel free
to download and copy the graph.)  I extended the activity to graphing the
surface temperatures of the planets as a function of distance from the
Sun, which led to the greenhouse effect discussion below, but now it
occurs to me that a great way to extend this activity would be to jigsaw
it: assign one group of students to graph size vs distance from the Sun,
another to graph temperature vs distance from the Sun, another to graph
density vs distance from the Sun, etc, and then the groups come together
to think about what it all implies for the formation of the solar system.

Second, when discussing the formation of the solar system and

describing how small grains of dust started to stick together, I

wanted to show a video clip but had some technical difficulties.  Here

is the link; start at 3 minutes into the video and go for 2.5 minutes.

(If you have time, the whole episode is worth watching.  It's from the

How the Earth Was Made series, which has some really nice

visualizations and is constructed around evidence, which is a key

feature missing from many science documentaries.  It tells science

like the detective story it is.  That's generally a good thing, but in

this case the implication that this particular astronaut doing this

particular demonstration singlehandedly saved the theory is a bit of

an exaggeration.)

Pocket solar system: https://nightsky.jpl.nasa.gov/download-view.cfm?Doc_ID=392

Peppercorn Earth: http://www.noao.edu/education/peppercorn/pcmain.html

Extrasolar planets: http://exoplanets.org/ has the most up-to-date

info. Even better, they have built-in graphing tools so you and

your students can easily explore the data.

Earth's surface temperature: I got my plot from the most authoritative

source for modern temperatures, NASA's Goddard Institute for Space Studies.

This link only scratches the surface of climate change data because it deals

with modern temperature measurements (as opposed to long-ago temperatures

inferred from ice cores etc) but as the greenhouse effect was not the focus of

the workshop I won't try to compile a list of links here.  (For those

not attending the workshop: we graphed planets' surface temperatures

vs distance from the Sun, and we saw the general pattern that farther

from Sun equals colder, but we also saw that Venus is a real outlier

from this pattern.  That's because Venus has had a runaway greenhouse

effect.  Earth also has a natural greenhouse effect which keeps us

from being frozen, but which is now being augmented by a manmade

greenhouse effect.  I did tell the teachers that Earth has a "carbon

cycle" which will absorb the extra carbon dioxide through the oceans

into rocks, but I forgot to mention that it will take hundreds of

thousands of years; I didn't mean to imply that humans can carry on

regardless. Venus' greenhouse effect is "runaway" because its

carbon cycle shut down when its oceans boiled.)

Finally, a few links I didn't get time to show but which will help you

appreciate the size of the universe (and the sizes of things in it):

the classic Powers of Ten video and an interactive tool.

One Plus z

This marks the launch of a new series of posts, aimed at astronomy and physics majors. In the course of my teaching I've noticed a few topics---such as propagation of errors and reduced mass---which seem to fall through the cracks between classes.  Students hear a bit about reduced mass in more than one class, but never seem to get a satisfying explanation in any one class.  Their lab instructor taught them how to propagate errors but never made them think about why.  And so on.  This first post is much more specific---how to think about redshifts and velocity dispersions in cosmology---but fits the bill because it seems to fall through the cracks between textbooks.  Practitioners know that "you need to divide by 1+z" but documentation of this is hard to come by.  So here we go.

In cosmology, we often want to measure the rest-frame velocity dispersion of a galaxy cluster, but what we actually measure is the redshift dispersion. How are they related? Redshift z is defined in terms of emitted and observed wavelengths as

This means that 1+z is a stretching factor; it is the ratio of observed to emitted wavelengths.  So you will see the combination 1+z over and over, rather than z by itself.  Get used to thinking in terms of 1+z!

The Doppler shift formula tells us the wavelength stretching factor in terms of velocity:

You will often see this called the relativistic Doppler formula, as opposed to the simpler low-velocity approximation used in many situations. But I suggest thinking of this as the Doppler formula because  high velocities are common in astrophysics, and this correct version is simple enough to memorize. Habitually using the low-velocity approximation can get you in trouble.

The Doppler formula can be inverted to obtain

Now imagine two galaxies, one at rest¹ in the cluster frame (with velocity v₁ in our frame) and a second moving with some velocity v₂₁ relative to the cluster which implies some velocity v₂ in our frame.  According to the Einstein velocity addition law,

Substituting the inverted Doppler formula into this, we obtain a complicated-looking expression for v₂₁/c:

which we can simplify in a few steps:

Because of my poor equation formatting, I have to remind you here that this is an expression for v₂₁/c, where v₂₁ represents a velocity in the cluster frame rather than in our frame. This gets us close to our goal because we want to know the velocity dispersion in the cluster frame. But this is as far as we can go without an approximation. A useful approximation in this context is that so define and eliminate z₂ using :

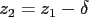Taylor expanding this about we obtain

This is true for any small redshift difference, so it must be true if delta represents the redshift dispersion of the cluster (thus making v₂₁ represent the velocity dispersion of the cluster). Therefore

However, there is a much more elegant way to derive the same result. Imagine a hypothetical observer on the first galaxy. Because of the definition of 1+z as the ratio of wavelengths, it must be true that 1+z₂ = (1+z₁)(1+z₂₁) where z₂₁ is the redshift of galaxy 2 as seen by galaxy 1 (z₁ and z₂ are, as before, redshifts seen by us). Therefore

Again we use an approximation: so that we can use the low-velocity approximation for the Doppler shift, . Therefore

which is the same result as before.  We don't actually need special-relativistic reasoning if we simply use the definition of redshift to isolate the one nonrelativistic velocity in the problem.

We can better expose the equivalence of these two approaches by taking the idea of daisy-chaining wavelength ratios and applying it directly to the Doppler law:

This just says that galaxy 2's wavelength ratio ("ratio'' here is relative to a laboratory standard) observed by us is its wavelength ratio observed by galaxy 1, times galaxy 1's wavelength ratio observed by us.   In a few lines of algebra, you can show that the above expression leads directly to the Einstein velocity addition law.  The addition law can be derived in more than one way, but to me this is the most intuitive way.  Thus, daisy-chaining Doppler factors and using the velocity addition law are not contrasting approaches; they are actually the same thing.

Exercise for the reader: show that the expression above does indeed lead to the Einstein velocity addition law.

Footnotes:
¹ I specify "at rest" here only so that later it will be easy to think of this galaxy’s redshift as the mean cluster redshift.