The Dating Game

Our third activity last Friday was on radioisotope dating.  (Everyone
has heard of carbon dating but carbon is just one of many radioactive
isotopes used for dating, and not even the most useful one for
geology, as we'll see below.)  This tied in with the other two
activities, because a certain age pattern in seafloor rocks was a
prediction generated by students' model of continental motions.  So
how do we measure the ages of rocks?

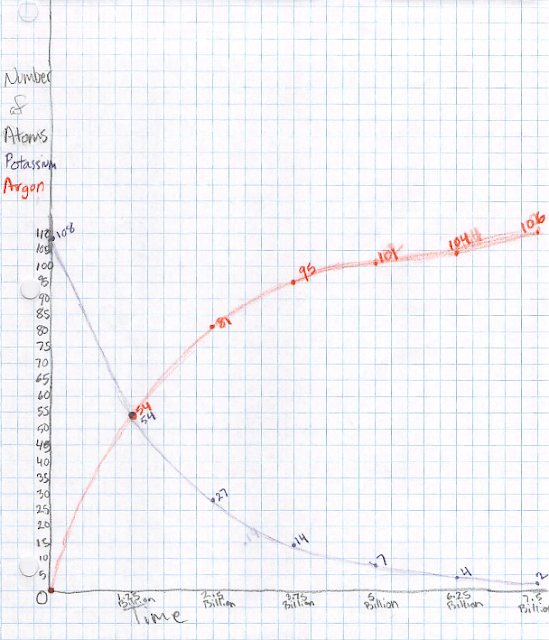
I prepared a whole bunch of small pieces of paper which were purple on
one side and white on the other.  Each group got a handful and put
them all purple-side up.  These represent potassium-40 atoms.  Each
group started constructing a graph of the number of potassium-40 atoms
vs time.  Let's say we start with 100 such atoms at a time we call
zero (we'll see later what this really means).  Over 1.25 billion
years, half of the potassium-40 atoms decay into argon-40 atoms.  The
students represent this by flipping over half of the "atoms" so the
white side is up.  Once flipped over, it can never flip back.  One
analogy is that once a ball rolls downhill, it's not going to roll
back up; similarly the argon-40 atom is in a lower-energy state.  (The
word "decay" evokes an irreversible process, for good reason.) So now
the student plots 50 atoms at a time of 1.25 billion years.  After
another 1.25 billion years, half of the remaining potassium-40 atoms
decay, so we now have 25 left and we plot that.  We may also want to
keep track of the number of argon-40 atoms, so (in a different color
pencil) we put zero of those atoms at time zero, 50 at 1.25 billion
years, and 75 at 2.5 billion years.

Keep going with this process.  In another time step, the 25
potassium-40 atoms decay into 12 or 13 argon-40 atoms. An atom can't
be half-decayed, and there is an element of randomness in this
process, so you can flip a coin or just decide randomly if it's 12 or
13.  (Aficionados will recognize that there is some probability of 11
or 14 as well, but that's beyond the scope here.)  Keep going until
you run out of graph paper, then connect the dots.

Now, how can we tell how old a rock is?  Look at the ratio of potassium-40 to
argon-40 atoms: 1:0 at the start, 1:1 at t=1.25 billion years, 1:3
at 2.5 billion years, 1:7 at 3.75 billion years, etc.  Measuring this
ratio provides an unambiguous estimate of the age of the rock.  I had
the kids field a few practice questions where I would give an age and
they would give a ratio or percentage, or vice versa. (If you're more comfortable
with percentages, as a percentage of the total potassium-40+argon-40 atoms, it's
100% potassium-40 at the start, 50% at 1.25 billion years, 25% at 2.5 billion
years, 12.5% at 3.75 billion years, etc.)

But what do we mean by the "age" of a rock? This is really key to
understanding the whole thing.  Argon is a gas, so when a rock is
molten the argon will just bubble out.  So when a rock solidifies, it
has no argon atoms, and a 1:0 ratio of potassium-40 to argon-40 atoms.
So t=0 corresponds to the last time that the rock solidified, which is
exactly the tool we need to date the age of new ocean floor oozing out
of the mid-Atlantic ridge!

The half-life of potassium-40 is well suited to dating rocks because
so many of them are so old.  What if we wanted to date something
younger, like a human skeleton from an archaeological dig?  Even if it
was 4000 years old, the ratio of potassium-40 to argon-40 would be so
close to 1:0 that we wouldn't be able to tell.  We need something with
a shorter half-life, like carbon-14, which decays to carbon-12 with a
half-life of only 5730 years.  Carbon-14 is great for dating
skeletons, but if we tried to use it to date a rock, we would most
likely find zero carbon-14 left so we would only be able to say that
it's many half-lives old.  To say that a rock is at least 10 of those
half-lives, or about 60,000 years old, is not very useful.

(Teacher warning: a lot of the implementation details are different
for carbon-14 dating.  For instance, there is never a 1:0 ratio of
carbon-14 to carbon-12, not even close. So adapting this exercise to
carbon dating would be tricky.)

This was a good activity for the 25 minutes we had left.  I wouldn't
try to squeeze this activity into any less time, but we definitely
could have used more time.  For example, we could have plotted the
ratio; used our computer skills to make plots, including of the ratio;
brought in some algebra to calculate things quickly through an
equation rather than graphically; etc.

Trembling in our Books

Yesterday we did three activities related to plate tectonics: making a
model of continental motion and generating predictions from it;
locating earthquakes; and radioisotope dating of rocks.  The second
activity followed roughly the reasoning outlined here.  However, I
didn't want to get into S and P waves, so instead of measuring the
distance from the epicenter to the seismograph by analyzing the wave
form, I decided to "simplify" and give students the time of arrival at
the three seismographs.  Only after we started the activity did I
realize that although the timing information I gave was sufficient,
some serious algebra would be required to solve the problem with just
that information.  So I ended up giving them the distance from the
earthquake to one of the seismographs, just to get them started.

Using timing information to solve for a location is an important
problem with many real-world aspects.  For example, GPS uses exactly
the kind of reasoning shown in the last figure of the page linked to
above, but in full 3-d with satellites distributed around the Earth,
to solve for your full 3-d location.  So I like the pure-timing aspect
of my version of the activity, but I have to find a way to make
workable for 5-7 graders.

Still, I don't think the kids noticed all this scrambling going on
behind the scenes.  They got the main ideas: the intersections of two
circles are the candidate epicenters based on two seismographs, and a
third seismograph can be used to resolve the ambiguity.  And they had
fun finding the mystery location of the epicenter.  I think we took
about 40 minutes on this activity, including a 5-minute opening
discussion on the link between earthquakes and our previous activity.

Get My Drift?

Yesterday we did three activities related to plate tectonics: making a
model of continental motion and generating predictions from it;
locating earthquakes; and radioisotope dating of rocks.

In the first activity, I gave students cutouts of the continents.
(The best way to find these is by googling terms related to this
activity; you can't just print a world map because of the distortion
inherent in most projections.)  The cutouts were on their desks as the
students filed in, so it was interesting to see what the students did
without any instructions: mostly arrange them as they are now rather
than try to put them together like a puzzle.  But it only took a small
hint to get them assembling the puzzle.  Once each group settled on a
way of fitting the continents together, I had them glue the model to
one side of a handout I had prepared.  On the other side they were
instructed to make four specific predictions about what would be
observable if this model were true.  I had to drop some major hints,
but the groups did eventually come up with the same four major
categories: (1) fossils on once-adjacent pieces of land should be the
same even though they are now very far apart; (2) living creatures on
once-adjacent pieces of land should be similar (making allowance for
evolutionary changes and for especially mobile animals such as birds
to be excluded from this analysis; (3) an expanding ocean floor should
be young in the middle where it spreads apart, and progressively older
near the continents (some groups put more emphasis on finding an
identifiable mid-ocean feature, but it's basically the same idea); (4)
once-adjacent pieces of land should have very similar older rock
layers even though they are now very far apart.  One thing no one got
even though I mentioned GPS is that we should be able to measure the
distance between, say, North America and Europe increasing very
slightly each year (it is, by a few centimeters per year).

I had planned for this to be iterative.  In my original plan the
groups were to make a very specific prediction such as "fossils found
in this part of Antarctica match the fossils in this part of
Australia", and then I would look that up quickly (to prevent
computers from being a distraction), and then after seeing how all
four predictions went they would make a better model on a new sheet of
paper (I brought lots of continent cutouts).  But the initial puzzle
assembling took much, much longer than I anticipated.  Some groups
took a lot of time to trim their rough-cut continent cutouts in
exquisite detail; others rearranged theirs many times; others just
didn't focus as much as I would have liked.  So we didn't go through
another iteration.  But one lesson that was clear to me at least is
that although South America fits nicely into Africa, almost nothing
else matches that clearly.  At some point you have to guess (this is
clear when comparing the different guesses of the different groups),
and at that point you have to look for fossil evidence to verify or
falsify your guess.  That whole process is what science is really all
about!

In the time left before break, I asked the students to guess why the
continents move.  They had a lot of crazy theories, but I steered it
back to what we had learned last week: the core of the Earth is hot,
heat flows to areas of lower temperature, and it can flow through
radiation, conduction, and/or convection.  We talked about how each of
these might or might not apply in this case, and figured out that
convection is well suited to transporting heat through the mantle,
which is fluid although not really molten.  Once we got this all into
a diagram with convection loops in the mantle, it was clear that this
was a very plausible mechanism for making continents move. 

This whole activity took 45 minutes, and as I mentioned I probably
should have budgeted much longer, and/or come up with ways to save
lots of time on the puzzle-assembly.  Devoting time to verify or
falsify specific predictions and come up with a better model would
have been a great illustration of the process of science.  Maybe it
should be a homework.  But, apart from this reservation, I think it's
a great activity.

Heat, Earth, and Sun

Friday I started earth science with the 5-7 graders at Peregrine
School. We started half an hour late because of the all-school
discussion of the meteor strike over Russia.  So I squeezed a lot into
35 minutes before a shortened recess break.  We reviewed the structure
of the Earth and then we talked about the three different ways heat
flows: conduction, convection, and radiation (which in this context is
just another word for light; it does not mean ionizing radiation,
which is what you need to protect your DNA from).  I brought a torch
and a saucepan to make the discussion of conduction more concrete:
cookware designers want the bottom to conduct heat very well so that
the food is heated evenly, but they want the handle to conduct heat
poorly so that you don't burn yourself.  Then I added water to segue
to convection.  Because hot fluids rise, convection occurs whenever a
fluid is heated from below, which occurs in very diverse contexts:
boiling water on the stove, fluid rock in Earth's mantle, and the
movement of air in the atmosphere.

Next, I drew a Sun far from our diagram of Earth, and I asked how heat
gets from the Sun to the Earth.  It can't be conduction or convection,
because empty space can't do either of these.  It's radiation (light).
So we observed thermal radiation (the light emitted by an object by
virtue of its temperature), noting the brightness and color of a light
bulb at different temperatures (achieved by changing the voltage).  We
analyzed the color in detail by looking through diffraction gratings
to make rainbows from the white light, and noting which color in the
rainbow was brightest.  The pattern that emerges is: raising the
temperature makes the light bluer, and makes it much brighter.  We
think of red hot as being about the hottest temperature we ever
encounter, but really white hot is even hotter (the light is a mixture
of red, green, and blue), and blue hot is even hotter than that.  (The
ocean and sky are blue because they scatter the blue light from the
Sun, not because they are emitting light.)  Even objects at room
temperature emit thermal radiation, but that light is "redder than
red" or infrared.  These kids had played with an infrared camera
before, so I didn't bring one, but we discussed their IR camera
experience in this new light.  (Read this post to get the basics of
the IR camera experience.)

The last point I made before recess break: Earth's temperature is a
balance between the energy it gets from the Sun and the energy
(infrared light) it emits into space.  To maintain a roughly stable
temperature, it must emit as much as it gets.  We would examine that
balance in more detail after the break.  During the break, I had a
trick to keep them thinking about this subject: I brought a parabolic
mirror, pointed it at the Sun, and we entertained ourselves setting
things on fire.

After the break, before moving on, I felt they needed more practice with
conduction, convection, and radiation, so I had them work in groups to design
thermoses.  We put together ideas from the different groups to arrive at a
consensus design which minimizes conduction, convection, and radiation.

Back to the main thread: I noted how the parabolic mirror gathered energy from
the Sun over a largish area and concentrated it on a small area.  If we
measured the power (energy per second) falling over one square meter
(about twice the area of the mirror), we would find that it's about
one kilowatt, or 1 kW.  I brought a 1 kW hair dryer to make that more
concrete.  We then talked about night vs day, and how the Sun is
fairly low in the sky during part of the day, and concluded that the
average power from the Sun on 1 square meter of Earth would be more
like 300 W.  So each square meter of Earth should emit about 300 W of
infrared light in order to maintain a stable temperature.

Recall that power emitted ("brightness") increases strongly as the
temperature of an object increases.  So if the temperature of that
square meter of Earth is low, it will emit less than it absorbs, and
that will raise its temperature.  But if the temperature goes up very
high, it will emit more than it absorbs, and the temp will come down.
We ought to be able to calculate the temp which is just right so that
it emits exactly 300 W.  This is where we returned to the computer
programming that the kids are loving so much.  Most of these kids are
not familiar with algebra, but they can (with lots of guidance from
me) write a loop over a range of plausible temperatures and print out
the power emitted at each temperature.

To do this, I had to give them the equation for power (in watts)
emitted as a function of temperature: 0.0000000567 T⁴, where T is in
Kelvins.  That led to a discussion of Fahrenheit vs Celsius vs Kelvin.
Fahrenheit is defined so that water freezes at 32 degrees and boils at
212, a 180-degree difference; Celsius is defined so that water freezes
at 0 degrees and boils at 100.  Therefore, each Celsius degree is
"bigger" by 180/100 or 9/5.  Therefore Fahrenheit = 9/5 Celsius + 32.
Kelvin = Celsius + 273 (I explained about absolute zero), so
Fahrenheit = 9/5 (Kelvin-273) + 32.  Admittedly, most students didn't
follow all these steps, but at least one did, and I told the others to
just use this to convert while focusing on the logical steps needed to
carry out their program.

So each group wrote a Python script to check from 1 to 1000 Kelvins,
at each step printing out the power emitted and the Fahrenheit
temperature.  It turns out that 26 F is the right temperature for 300
W.  Is this a reasonable answer?  We discussed the approximations
involved (primarily albedo, using snow as an example).  Then we tried
representing this information graphically.  Instead of scanning a list
of numbers to find the right temperature, I taught them how to make a
graph of power emitted vs temperature.  We then added a horizontal
line at 300 W, and the temp at which the line intersects the curve is
the "right" temp.  I really want to work on graph-making and
-interpreting skills, so we discussed the labels we should put on each
axis, and how to summarize the plot in words.

As a teaser for next week, a slightly more rigorous calculation shows
that Earth's global average temperature should be even colder than 26
F.  The reason we are not in fact that cold is that our atmosphere
intercepts some of the outgoing infrared light and turns it back to
the surface: the greenhouse effect.  There is a natural greenhouse
effect which makes our planet livable.  The kids had of course heard
of the greenhouse effect and global warming, so they were able to see
right away that the problem is not the greenhouse effect per se; it is
that we are adding to the natural greenhouse effect, resulting in too
much of a good thing.  More on that next week.

The original plot we made:

and a zoom in to the important part:

Great Balls of Fire

This is a great thing about a small school: they can quickly
reconfigure to take advantage of learning opportunities.  I visited
Peregrine School for other reasons on Friday morning, but a meteor had
just injured over 1,000 people in Russia.  Students in all grades had
been assembled for chorus anyway, so right afterward I explained a bit
about the meteor and took many, many questions. 

I'm not going to write much here; the New York Times ran
excellent coverage (check out the pictures and video there, as well as the
articles listed under "Related").  If you just want to see some video,
here is a good collection of about four short videos which capture
different aspects such as the brightness of the flash, the eeriness
of the shadows, and the loudness of the boom.  After showing a few
quick videos to the kids, I really didn't say much; I just took
questions.  This was a great idea, because the kids eagerly presented
me with a fantastic variety of questions.

This was a great example of how the scientist-in-residence idea can
work well for a school.  Schools and scientists should do more to
cultivate long-term relationships with each other.

[If you want to know why there are rocks in space, here is a great visualization
of how very small grains of rock came together to form bigger rocks and
eventually planets in the early days of the solar system; some rocks still haven't
yet slammed into a planet because space is really, really big.]

Toy DNA Analysis Part III: Eve of Reconstruction

After the first and second activities of the morning, there was not
much more than 30 minutes left.  I wanted to do an activity with
mitochondrial DNA, so I went over the background first. (They had seen
much of the following earlier in the year, but the review turned out
to be necessary.)

Each cell has a nucleus which contains DNA, surrounded by the bulk of
the cell ("cytoplasm") which has various structures ("organelles") for
performing various functions.  One type of organelle is mitochondria,
when help you turn oxygen into energy.  Each cell has many
mitochondria, and here is the amazing thing: they have their own DNA!
They are not built according to instructions recorded in the DNA of
the nucleus; they simply reproduce by dividing asexually, as if they
were self-contained cells within the cell.  When the cell itself
divides, each daughter gets half the cytoplasm and therefore half the
mitochondria.  It is thought that mitochondria were once independent
bacteria, which learned to cooperate so well with other cells that
they took up residence.  That's pretty amazing!  Another amazing fact
is that all creatures on Earth share the same DNA code.  We are all
related, even humans and yeast.  (Example: if you put the DNA letters
for human insulin in yeast, the yeast understand those instructions
perfectly and makes human insulin.)

When a human egg cell is fertilized, the sperm carries in half the
nuclear DNA to complement the mother's half of the nuclear DNA.  But
the egg has an enormous amount of ctyoplasm and the sperm contributes
none.  So your mitochondrial DNA is an exact replica of your mother's,
and of her mother's, and of HER mother's....there is no shuffling with
each generation as we have with nuclear DNA.  Thus, mitochondrial DNA
makes it much easier to test whether you are a direct descendant
(through an all-female line) of, say, Cleopatra.  (A similar thing can
be done with Y chromosomes and all-male lines of inheritance.)
Furthermore, by mapping the geographical distributions of
mitochondrial DNA, we can trace out migrations of women over time.
(Ditto for Y chromosomes and men.)

It's good to ask the kids a few questions to see how well they
understand.  In this case, a girl said she was sorry for boys because
they had no mitochondria.  So we discussed that issue again: everyone
has mitochondria (that's how they turn oxygen into energy) but boys
won't pass theirs on to their kids.  Moms really do contribute more
than half, as immortalized by this song.

But there can be mutations. It turns out they're fairly rare in
mitochondria, probably because most mutations would be fatal very
early on.  But they do happen.  So if we gather mitochondrial DNA from
a large sample of people, we will find sequences that differ by a
little bit.  We should be able to trace the mutations backward and
reconstruct ancestor DNA.  For example, if we saw sequences GATTACA,
GATTACT, and AATTACA, we might guess that the ur-grandmother, many
generations back, of all three people had the sequence GATTACA.  One
mutation somewhere along the line would explain the people with
GATTACT, a different mutation somewhere else along the line would
explain the people with AATTACA, and the people who had never
experienced a mutation along their line would still have GATTACA.
They hypothesis of, say GATTACT being the ancestor is much less likely
because it requires that there was one mutation to make it GATTACA and
then, in the line with this mutation already present, there was
a second mutation making AATTACA.

So here's the problem I posed to the kids: reconstruct the ancestor of
these sequences:

CATTACGACT     
GAATACGACA      
GATTACAACT      
GATTACGACA      
GATTACGACT      
GATTATAACT
GATTCCAACT      
GTTTCCAACT      

Go ahead: print these out and cut them into strips, try to arrange
them as leaves of a tree, and guess what the branches and trunk have
to look like.

Some groups were lost, and so I tried to work it out with them on the
board, starting by making a guess about the immediate ancestor of one
very similar pair.  It turned out this was probably a bad guess,
because once we had worked out two hypothetical ancestors of two
different pairs, those two hypothetical ancestors seemed to have very
little in common, whereas we would have expected them to look similar
enough that we could guess a hypothetical original ancestor which
spawned them both.  Just as I was realizing that we were almost out of
time, another group handed me a sheet of paper in which they had
worked it all out.  The lesson I drew for everyone: don't be afraid to
take a guess, work out the consquences of that guess, and if it
doesn't work, scrap that guess and start over.  That's what science is
all about! (See the first minute or so of this video.)  Just because
lunchtime was coming up fast does not mean that we had done anything
wrong.  The wrong thing would be to continue pushing a guess which
doesn't explain all the evidence.

If I do this activity again, I would print out very large copies of
the sequence so I could rearrange them easily on the board (writing
with chalk does not lend itself to rearrangement).  Or I would print
it at regular size and use a document camera.  I would probably also
walk them through a simplified example first as I did in writing this
post.  Another idea I just had is to try representing the information
differently.  Perhaps a color code instead of letters would make
things just jump out. 

I saved a few minutes for the coolest part of this: because we know
that mutations happen about once every 10,000 years, we can use this
as a clock.  In my simplified example, you have to reverse-engineer
three mutations to get back to a common ancestor which explains all
the data.  That makes 30,000 years.  In real life with real data, you
have to go back 200,000 years, but you can do it.  That means that
there was one female about 200,000 years ago from whom every human
alive today has inherited their mitochondrial DNA; she is called
mitochondrial Eve.  This doesn't mean that other females living at
that time didn't contribute to people alive today; they surely did,
through their nuclear DNA.  But mitochondrial Eve is the only one who
has an unbroken female line to anyone alive today.  And a similar
argument identifies "Y-chromosomal Adam" who lived around 100,000
years ago.  We are all intimately related!

Toy DNA Analysis Part II

After the first activity and recess break, I posed the challenge of
finding out which animal is most closely related to the hippopotamus.
I gave them short (400-base) DNA sequences of various mammals and
asked them to figure out which was most similar to the hippo's.
Again, I just made up these short sequences to keep it simple.  In
real life, there are a lot more complications just as varying number
of chromosomes, billions of base pairs, etc.

The bottom line is that they had to take an animal, look at each
position in the sequence, ask whether that that animal's DNA at that
position was different from the hippo's, and total up the differences.
After repeating this for several animals, they would see which one had
the least differences.  After the near-chaos of the morning's first
activity, I thought it would be a good idea to go over the big picture
and assemble some pseudocode on the board based on their ideas:

get hippo dna
for each animal other than hippo:
    get this animal's dna
    compare this animal's to hippodna
    print number of differences

I emphasized basic ideas like what do we want to put inside the loop and what do we want to put outside the loop. A program like this does it:

hippodna = open('hippo.txt').read()
nletters = len(hippodna)

for filename in ('cat.txt','dog.txt','rhino.txt','bluewhale.txt','rockhyrax.txt','rhesusmonkey.txt'):
    dna = open(filename).read()
    differences = 0
    position = 0
    for letters in hippodna:
        if hippodna[position] != dna[position]:
            differences += 1
 position += 1
    print filename,'has',differences,'differences with hippo dna' 

Yes, Python experts, I know there are more efficient ways to do it but this seems most straightforward for a kid. I won't go into the detail I went into for the morning's first activity, but it was a similarly intense back-and-forth with students running into an obstacle every 30 seconds, which I tried to turn into a learning experience. They again needed emphasis on proper indenting, punctuation, remembering that if they named a variable 'difference' early on then they couldn't refer to it as 'differences' later on, etc. They again wanted to do one animal at a time rather than write a loop. But it was a really good learning experience.

This took close to an hour. At the end, we discussed how they might modify the program to see what's most closely related to some other mammal, and then a third mammal, etc, and build up a picture of how everything is related to everything else: a family tree. That was the emphasis of the morning's third activity.

Toy DNA Analysis Part I

Last time I visited the 5-7 graders at Peregrine School, I introduced
the idea of computer programming languages (specifically, Python) as a
way of automatic repetitive tasks.  That sounds boring, but I made it
interesting by building the activity around an inherently interesting
challenge---cracking a code---which happens to have a repetitive
aspect---translating each letter of a long message after you've
figured out the substitution pattern.  At the end, we had a little
time to discuss how DNA is a code, which is the connection I really
wanted to make to what they had already learned in biology.  This
week, we were poised to take it much further with three data analysis
challenges, two of them requiring Python programming.  As a result,
I'm going to split the morning's activities into three separate blog
entries.

The first challenge was to rescue a baby.  Some babies are born with a
genetic defect which does not allow their body to process the amino
acid phenylalanine.  If they don't follow a strict low-phenylalanine
diet, it builds up in their body and causes brain damage (mental
retardation) within the first year of life.  So there is a very strong
motivation to find out if the baby has this condition very soon after
it is born!  In practice, there is a blood test which does not involve
analyzing the DNA itself, but I framed the problem as one of DNA
analysis.  I made up long DNA sequences for about 15 babies, and asked
them to write a program which would look at a certain location within
each sequence, and print an alert if the sequence was not normal.  To
keep things simple, I just made up a simple condition for "normal":
the three letters starting at position 399 should be "GAT".

They had forgotten a lot in the two weeks since my first visit.  I
would normally recommend much more frequent visits for teaching
programming, but I was sick last week.  Still, they were very into it.
They wracked their brains trying to remember things, but I had to give
a refresher tutorial on for loops and if statements.  It took almost
an hour for everyone to finish completely, and there was again a
friendly competition to see who could finish (identify the sick baby)
first. 

The evolution of their programs was fascinating.  One group thought
they were done when they had something like:

dna = open('jane.txt').read()
print dna[398:401]

Even this simple program has a lot of ideas in it.  For example, doing
the subscripting correctly requires thinking about: (1) position 398
is actually the 399th position because Python starts counting at
position 0 rather than position 1; (2) 398:401 means up to but not
including 401; (3) you can't write dna[398-401] because the arithmetic
operation 398-401 yields -3, and Python will interpret this as 3
positions before the end of the sequence.  There was a lot of
interaction between me and the kids on each of these points.

In any case, when the first group had gotten this far, they thought
they were done.  They would just change jane.txt to john.txt, rerun it
to see if John was sick, repeat for Joan, etc, and just read off the
screen whether it said 'GAT' for that baby.  This would work ok for
the 15 examples I brought, but PKU (the aforementioned disease) is
present in only about 1 in 15,000 babies, so they really needed to
automate a loop over all the babies.  They initially thought I was
moving the goalposts, but the other groups agreed that this first
group was not really done.  So they started working on a loop:

names = ('jane.txt','john.txt','joe.txt')
for name in names:
    dna = open(name).read()
    print dna[398:401]

I had to repeat many times the importance of proper indentation so that it's clear
(to the computer and to a human reading the code) which actions get
repeated for each name, and which actions only get done once.  A
common mistake is

names = ('jane.txt','john.txt','joe.txt')
for name in names:
    dna = open(name).read()
print dna[398:401]

which prints only the last one, after cycling through all the names. Notice that I typed in only three names to make sure my loop would work, before bothering to type in all 15 names. In fact, I taught them how to avoid typing in any names by grabbing all names that fit a certain pattern:

import glob
names = glob.glob('j*.txt')
for name in names:
    dna = open(name).read()
    print dna[398:401]

I briefly discussed how it can be incredibly time-saving to import some functionality that someone else has already written. But back to the main point, the fastest group now thought that they were really done: this program would print "GAT" for each healthy person, and they just had to scan the output for something other than GAT. But, I asked them, how would they know which person had that abnormal sequence? They tried adding to the end of their program:

import glob
names = glob.glob('j*.txt')
for name in names:
    dna = open(name).read()
    print dna[398:401]
    print name

But this gives output like:

GAT
jane.txt
GAT
john.txt
GCT
joe.txt
GAT
jim.txt
GAT
...

and they incorrectly interpreted this as John having GCT, because they hadn't paid attention to the fact that they asked the computer to print the DNA first, and then the name. An important rule of programming is to make your output clear. Things which belong together should be printed together. A much better print statement is:

print dna[398:401], name

which keeps it to one line per baby:

GAT jane.txt
GAT john.txt
GCT joe.txt
GAT jim.txt
...

Now they really thought they were done, but I pointed out that they were looking for 1 in 15,000 babies, and they couldn't count on a human to scan a list of 15,000 lines which say 'GAT' and not miss an abnormal one. They really need to print out just the sick ones with a very clear warning:

import glob
names = glob.glob('j*.txt')
for name in names:
    dna = open(name).read()
    if dna[398:401] != 'GAT':
       print name, "is sick"

Now they were done: the output is simply

joe.txt is sick

I took a few minutes to talk about the subtleties of combining if's, for example the difference between

if dna[398] != 'G' and dna[399] != 'A' and dna[400] != 'T'

vs

if dna[398] != 'G' or dna[399] != 'A' or dna[400] != 'T'

Surprisingly (to me at least), they found this last point very easy. As I said, this whole activity took very nearly an hour. (I had saved a bit of time by preloading their computers with the data files.) It was highly interactive, and if there had been much more than three groups having another knowledgeable adult in the room probably would have been a good idea. I'm not going to pretend that as a result of this activity the kids have actually mastered even the very basics of programming, but it was good practice in logical thinking, and it's clear that with continued practice I will eventually get them doing some real data analysis. One good sign: one of the girls continued programming throughout the recess break following this activity!